一、设计情境 得出基本模型
下图是停车场和售票厅的相对位置,为了在旅游高峰期尽快到达售票厅排队买票,你们会在人行小路的哪个位置横过小路使得所走的路程最短?

[设计意图]设计旅游景点作为背景,激发同学们兴趣和求知欲,要想快速到达售票厅,则需要将实际问题转化为数学问题. 然后继续追问如何转化,突出转化过程中正确建立模型的重要性。
分析:把售票大厅和停车场分别抽象为A,B两点,人行路抽象为直线I,建立模型如下,问题就转化为求在直线I上存在的P点,使得AP和BP的距离和最短。
依据:两点之间,线段最短,直接连接A,B两点与直线I有个交点,
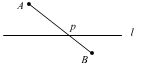
就是p点。
归纳:像这种两点处于一条直线异侧的类型,做起来很简单,我们把这种最简单的最短路径问题的模型作为基本类型。用来类比其它的最短路径问题,然后加以转化,达到使复杂的问题简单化的目的。
二、设计情境 得出将军饮马问题
如图,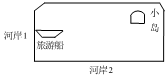
湖的河岸1处的旅游船先前往河岸2的渡口接游客,然后将游客送往小岛上游览,请问工作人员把渡口设定在河岸2的何处?使得其路径最短,才能达到节约成本的目的。
[设计意图]把历史上有名的将军饮马问题设计到旅游景点的娱乐项目里,激发同学们的学习兴趣和求知欲。引导学生把这种类型转化为基本类型的思维方向,突出本节课的重点。
把实际问题转化为数学问题,建立模型如下:
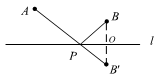
把旅游船和小岛抽象为A,B两点,河岸2抽象为直线I,实际问题就转化为求在直线I上存在的P点,使得AP和BP的距离和最短。这个P点该如何确定?
来类比基本类型,类型二的两点在同侧,类型一的两点在异侧,
那么我们需要把其中一个点转移到直线的异侧,转移一个点到直线异侧的条件是:不能改变各条线段的长度,简单说就是要全等变换。全等变换的方法除了轴对称,还有平移和翻折。以转移B点为例,作B点关于直线I的垂线,截取OB=OB',B'点就是B点的对称点,根据轴对称的性质:对称点到轴对称上任何一点的距离都相等。直接连接AB',与直线I的交点就是P点,所以旅游船的最短路线是A→P→B。
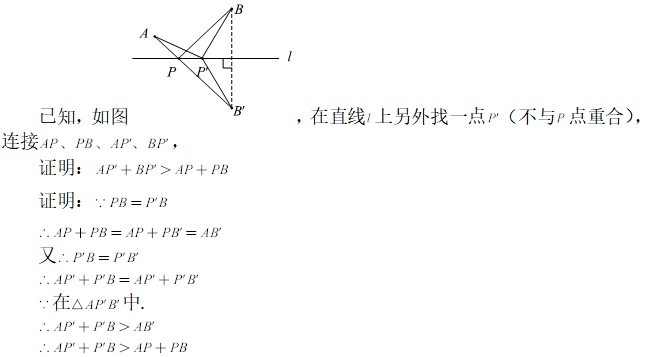
依据:三角形的两边之和大于第三边,无论在直线上哪个位置找一个与P点不一样的点,都要比AP+PB的距离和长。
其实像这种模型的最短路径问题,在数学上把这种最短路径问题称为“将军饮马问题”。
唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河。”诗中隐含着一个有趣的数学问题如图,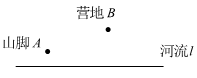
诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后再到B点宿营。请问怎样走才能使总的路程最短?
三、设计情境 运用新知
如下图,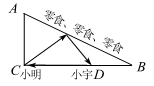
大家围在一起坐下休息(如AC,BC),把带去的零食摆成一条(如AB),小明坐在C处,他想先去拿零食,再去和坐在D处的同学小宇说话,最后回到C处,请帮他找出他的最短行走路线。
[设计意图]让学生把实际问题与数学紧密联系起来,从而在心中留下“生活中处处皆数学”的印象,凸显数学学科的重要。
首先建立数学模型,如右图。根据题意,CD路程是确定的。
实际就是问你小明在哪里拿零食,路线最短,这就是将军饮马问题。
[解法点评]找对称点,把点转移到对称点后,求对称点和D点的最短距离,根据“两点之间,线段最短”,直接连接对称点和D点与AB的交点就是要找的P点。
四、知识迁移1 最值题型
已知:如图点A(3,4),点B为直线X=-1上的一点,点B的坐标为(-1,1)时,在轴上另取两点E,F且EF=1,线段EF在X轴上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标。

[设计意图]考察学生解决问题的能力,使学生熟练地把最短路径问题与最值题型衔接起来,强化知识点。
知识迁移2 建桥选址问题
如图,某景区为了增加景点特色,在景区修建了一条两河岸平行的人工河,凉亭A,B位于河两岸,为了游玩通行方便,现计划要在河上造一座桥(桥垂直于河岸),使凉亭A,B之间的路程最短。已知河宽为100m,凉亭A到河岸M的距离为800m,凉亭B到河岸PQ的距离为400m,且凉亭A,B的水平距离为1600m,请计算从凉亭A出发经过桥后到达凉亭BD的最短路程。
解:如图,作点A到河岸的垂线,分别交河岸MN,PQ于点E,G,在AG上取AF=CD,连接FB,FB交PQ于点D,在D处作到对岸的垂线DC那么DC就是造桥的位置,此时从凉亭A出发经过桥后到达凉亭的路程最短。
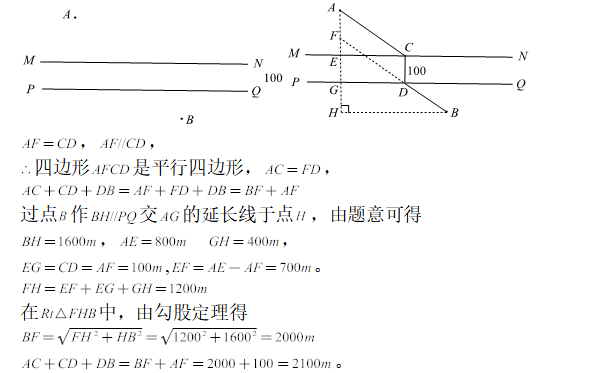
答:从凉亭A出发经过桥后到达凉亭B的最短路程为2100m。
[设计意图]在实际问题的基础上进行迁移,实现“不仅会找最短路径,而且还能灵活运用最短路径”的目标。
其实,最短路径的数学模型并不是一个,而是一系列模型的统称。课本的例题只是构建了基本模型,由基本模型衍生出一系列的模型,把此类问题的基本模型讲透,用熟,再逐渐利用基本模型去解决衍生模型,引导学生总结解决实际问题转化数学问题的规律:从同类事物中抽象本质特征→基本类型→类比、转化→认识新类型→解决问题并反馈。在实践教学活动当中,教师应该突破课堂教学的限制,将实践活动范围延伸至实际生活当中,促使学生在实践的过程中完成知识的内化任务,并在实践过程中获得更多解决问题的方法,强化学生的实践能力和创新能力,满足学生创新能力的培养需要。
参考文献
[1]张静,利用对称探求最值——— 从“将军饮马”谈起,中学数学月刊。
[2]许秋,“将军饮马”问题的五种解答策略,数理化学习(初中版)。





