1 引言
发动机的数学模型分为稳态模型与动态模型,稳态模型主要应用于发动机慢车以上状态的性能计算、参数设计等。动态模型涵盖了发动机由零转速状态加速到慢车状态的地面起动过程、慢车以上加减速过程以及空中起动过程。相比于稳态过程及慢车以上加减速过程,发动机起动过程更为复杂,涉及到起动机、燃油调节系统与发动机各个部件之间的协同工作,同时各个部件工作在远离设计点工况的状态,对外部条件十分敏感,容易出现燃烧室点火失败、压气机喘振、转速悬挂等各类起动故障。因此,建立一个相对准确的发动机起动性能计算模型,对于研究发动机起动过程性能、解决起动过程中遇见的问题,优化发动机起动控制规律等具有重要的理论意义及工程实用价值。
2 涡轴发动机部件级模型
本文的起动过程模型是在某型涡轴发动机慢车状态以上部件级模型的基础上建立的。某涡轴发动机由进气道、组合压气机、燃烧室、燃气涡轮、动力涡轮和排气喷管等部件组成,先建立各部件的数学模型,再根据各部件的流量、压力和功率等共同工作条件,列出一组共同工作方程,求解方程组即可得到发动机的状态参数[1]。
3 涡轴发动机起动过程建模
3.1 起动仿真算法
起动仿真算法的实质就是求取一组旋转部件的压比,使其满足选取的平衡方程。对于本文所建的涡轴发动机模型而言,其流量平衡方程为:
(1)燃气涡轮出口流量等于燃气涡轮进口流量与冷却气流量之和:
WGT,out-WGT,in-WGT,cool=0
式中,WGT,out为燃气涡轮出口流量,WGT,in为燃气涡轮进口流量,WGT,cool为燃气涡轮冷却空气流量。
(2)动力涡轮出口流量等于动力涡轮进口流量与冷却气流量之和:
WPT,out-WPT,in-WPT,cool=0
式中,WPT,out为动力涡轮出口流量,WPT,in为动力涡轮进口流量,WPT,cool为动力涡轮冷却空气流量。
(3)通过排气喷管的流量等于排气喷管进口流量:
Wnozzle,out-Wnozzle,in=0
式中,Wnozzle,out为通过排气喷管的出口流量,Wnozzle,in为排气喷管的进口流量。
转子动力学方程为:
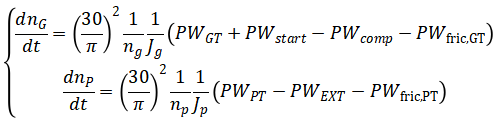
式中,Jg和Jp分别为燃气发生器转子和动力涡轮转子的转动惯量,PWGT为燃气涡轮功率,PWstart为起动机功率,PWcomp为压气机消耗功率,PWfric,GT为燃气发生器转子摩擦损耗功率,PWPT为动力涡轮功率,PWEXT动力涡轮轴引出功率,PWfric,PT为动力涡轮转子摩擦损耗功率。
动态迭代计算使用经典的Newton-Raphson算法求解,求取组合压气机压比πcomp、燃气涡轮落压比πGT与动力涡轮落压比πPT,使上述流量平衡方程满足精度要求。
3.2 低转速部件特性构建
为了准确模拟涡轴发动机的起动过程,需要获得准确的慢车以下状态的部件特性,而慢车以下状态的部件特性难以通过试验的方式获得,因此目前通常采用从慢车以上状态的部件特性外推的方法来获取低转速下的部件特性。本文利用基于相似理论的指数外推法[2],由发动机慢车以上状态的部件特性外推出其起动低转速状态下的部件特性。通常,低转速部件特性还需要利用试验数据进行修正,以提高起动模型的精度。
3.3 燃烧效率修正
在发动机的起动过程中,尤其是点火后的一段时间内,燃烧室的油气比和进口气流条件均偏离设计点状态较远,燃烧效率远低于设计点的燃烧效率。因此,在建立起动模型时,需要综合考虑燃烧室的油气比和进口气流条件的影响,对燃烧室模型的燃烧效率进行修正。起动过程中燃烧室的燃烧效率可以按以下公式估算[3]:
![]()
式中,ŋB为燃烧室的燃烧效率,ŋB,ideal(θ)为未考虑油气比影响的燃烧效率,△ŋB为燃烧效率修正项,其大小与油气比fa有关,θ为燃烧室进口空气负荷系数,其表达式如下:
![]()
式中Pcomb,in,Tcomb,in,Wcomb,in,分别为燃烧室进口的总压、总温和流量。
3.4 热惯性修正
发动机在工作时,气流与涡轮叶片以及机匣壁面之间存在大量的热量交换。发动机起动过程点火至慢车的过渡阶段,燃烧室和涡轮的气流温度急剧上升,气流和燃烧室以及涡轮的热量交换更为剧烈,将显著影响燃烧室和涡轮的出口温度。因此,在建立涡轴发动机的起动模型时,需要考虑热惯性的影响,对燃烧室和涡轮的数学模型进行修正,以保证起动过程中燃烧室和涡轮的出口温度和试验数据保持一致。下面以燃气涡轮为例,介绍热惯性模型的计算方法。
起动过程涡轮、机匣与燃气之间的热交换十分复杂,本文对其作如下简化:
(1)将涡轮分为叶片与机匣两部分简化处理,即动叶与静叶以叶片简化处理,涡轮盘与机匣以机匣简化处理。引入两个平均温度建立热惯性模型。
(2)燃气与涡轮部件之间存在热传导、热对流、热辐射等多种换热方式,本文引入复合换热系数集中处理换热量。
考虑热惯性影响后燃气涡轮的实际出口温度为:
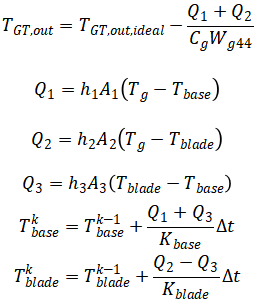
式中,TGT,out,ideal为未考虑热惯性影响的燃气涡轮出口温度,Cg为燃气平均比热,Wg44为燃气涡轮出口燃气质量流率,hi为复合换热系数,Ai为换热面积,Tg为燃气理想平均温度,Tbase为涡轮机匣/盘平均温度,Tblade为涡轮叶片平均温度,Tbase和Tblade分别为机匣/盘和叶片的热容,k表示第k步,△t为仿真步长。
动力涡轮的热惯性修正方式和燃气涡轮相似,燃烧室的热惯性修正则简单一些,只需要考虑气流和燃烧室壁面的热量交换。
3.5 温度传感器修正
某型涡轴发动机的数控系统采用热电偶测量燃气涡轮出口温度,由于热电偶与气流进行热交换至温度稳定需要一定的时间,因此,燃气涡轮出口温度的测量值与实际值相比,存在一定的滞后。而在发动机起动过程中,气流温度变化十分剧烈,热电偶测量温度的滞后尤为明显。为了使仿真结果更接近于实际发动机的试车数据,需要在起动模型中增加一个温度传感器模型,对燃气涡轮出口温度进行修正。简易考虑,温度传感器可采用一阶惯性环节表示[4]:
Tc=Tg-(Tg-T0)e-t/τ
式中Tc为温度传感器的测量值,Tg为气流的实际温度,T0为初始温度,t为响应时间,τ为时间常数。
3.6 总压恢复系数修正
发动机在起动过程中,具有转子转速低,流量小,各个旋转部件的压比均较低的特点,相比于慢车以上,其总压恢复系数更接近于1,且会随着转速的增加而逐渐减小,直至达到慢车以上状态时基本保持不变。因而,需要对总压恢复系数进行修正,具体修正方法如下:
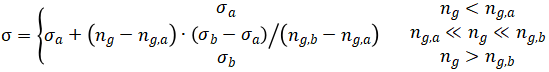
式中,ng为燃气发生器转子转速,ng,a和ng,b分别代表点火瞬时状态和慢车状态的燃气发生器转子转速。
4 仿真结果
为了验证上面建立的起动模型的精度,将某型涡轴发动机某次地面试车时的供油量数据与环境参数作为输入条件,模型仿真结果与试验对比如下图所示:
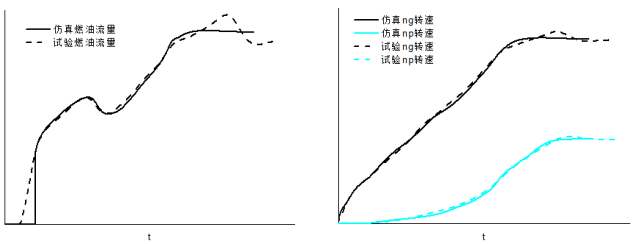
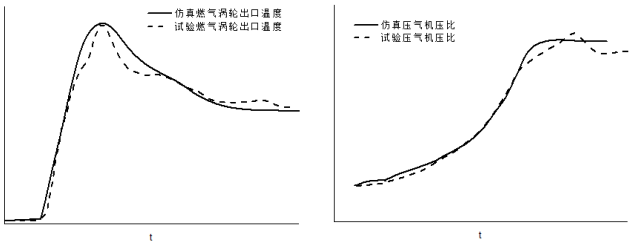
在模型中,点火转速前的供油量赋值为0,因此会使仿真出的供油流量在点火时的出现阶跃情形。从图中可以看出,在相同的供油流量条件下,达到慢车转速以前,模型仿真出的燃气涡轮、动力涡轮转速ng和np以及组合压气机压比与某型涡轴发动机的试车数据相比,吻合较好,误差在10%以内。燃气涡轮出口温度在峰值附近,仿真结果和试验数据存在较大的误差,但二者总体趋势相同,峰值温度和峰值出现的时间也基本一致。
5 结论
本文建立了某涡轴发动机的部件级起动模型,可模拟台架状态下发动机从转速近似为零的状态下加速至慢车状态的全过程。起动模型通过外推得到低转速下的部件特性,并综合考虑了起动过程油气比和进口气流条件对燃烧室燃烧效率的影响,燃烧室与涡轮的热惯性,温度传感器测量的滞后以及各部件总压恢复系数的变化。模型具有较好的仿真精度,可以在该模型上开展起动控制规律优化等研究。
6 参考文献
[1]周文祥.航空发动机及控制系统建模与面向对象的仿真研究[D].南京:南京航空航天大学,2006.
[2] Sexton W R. A New Method to Control Turbofan Engine Starting by Varying Compressor Surge Valve Bleed[D].Thesis for Master's Degree of Virginia Polytechnic Institute and State University, 2001: 14~66.
[3] Karpman B,Shade J L,Kane D E. Controlling Turbine Blade Tip Clearance According to Thermal Growth Model[P]. EP: EP1314857,2006.
[4]徐一新,万泓,余新春.基于实时时间常数的热电偶动态误差校正.传感器技术,2001,20(5):31~33.





