一、引言

国债收益率曲线，特别是10年期国债到期收益率，被视为固定收益投资市场的核心指标，其变动深刻影响着市场波动与资产配置策略。本文旨在探讨利用非结构化VAR（向量自回归）模型结合精选宏观经济指标，对10年期国债收益率进行预测的有效性和实际应用价值。通过系统分析多个宏观经济指标的组合效应，我们发现社会融资规模存量同比增速、核心CPI（消费者价格指数，不含食品和能源）以及美元兑人民币即期汇率能够构建出稳定的预测模型，为未来的国债市场走势提供前瞻性洞察。

二、VAR模型在国债收益率预测中的应用

（一）VAR模型特性概述

VAR模型，全称为Vector Autoregression模型，即向量自回归模型，是一种用于时间序列分析的统计模型。该模型最初由克里斯托弗·西姆斯（Christopher Sims）在1980年提出，并广泛应用于宏观经济学、金融领域以及其他时间序列数据分析的领域。VAR模型的基本思想是将所有的变量都视为内生变量，并假定每一个内生变量都可以由过去若干期的所有内生变量的线性组合表示。VAR(p)模型的一般形式可以表示为：

Yt= c + A1Yt−1 + A2Yt−2 + ⋯+ ApYt−p + ϵt

· 其中：Yt 是一个 k×1 的向量，表示包含k个内生变量的列向量在t时刻的观测值；c是k×1的常数向量；A1 , A2 ,…, Ap均是k×k的矩阵，称为滞后系数矩阵，分别表示Yt−1,Yt−2,…,Yt−p对Yt的影响程度；ϵt是一个k×1的误差向量，代表扰动项；p是滞后阶数。

VAR模型作为一种数据驱动的经济分析方法，其非结构化特性赋予了其独特优势：不依赖于严格的经济理论框架，直接从时间序列数据中提取变量间的动态关系；将所有变量视为内生，简化了模型设定过程，体现了经济系统的整体性；通过多方程联立结构，全面展现变量间的相互影响；结合脉冲响应与方差分解技术，深入剖析冲击的传导机制及其对系统整体的影响。

（二）数据选择与预处理

本文选取自2016年1月19日（1年期MLF首次操作）以来的中债10年期国债到期收益率月末值，以及同期月度宏观经济指标数据作为研究样本。在广泛筛选的基础上，通过相关性分析剔除了与10年期国债收益率相关性较低或统计上不显著的指标（如工业增加值、M1同比增速、CPI等），最终确定了包括社会融资规模存量同比增速、核心CPI同比增速、美元兑人民币即期汇率在内的关键变量。具体筛选数据如表1所示：

表1：10年期国债收益率与宏观经济指标相关性分析

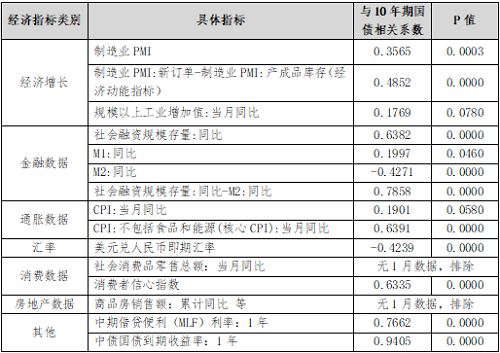
（三）模型构建与检验

平稳性检验与协整分析：为确保模型的有效性，首先对各变量进行平稳性检验，并通过Engle-Granger协整检验验证变量间是否存在长期稳定的协整关系。结果显示，社会融资规模存量同比增速、核心CPI同比增速、美元兑人民币即期汇率与10年期国债到期收益率之间满足1阶协整关系，适合用于构建VAR模型。

VAR模型建模：利用Python的statsmodels库中的VAR函数，对筛选出的变量进行VAR模型建模。通过AIC信息准则，并代入不同滞后阶数（1、2、3）检验模型的统计结果，确定模型的最优滞后阶数为2（如图1），以平衡模型的拟合优度与复杂度。

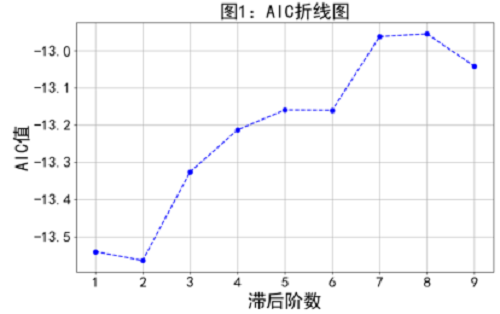
模型有效性检验：对构建的VAR模型进行残差相关性检验（表2）和DW（Durbin-Watson）检验（表3），以验证模型的稳定性和残差序列的独立性。结果表明，模型通过了相关检验，具有良好的统计性质。

表2：四变量残差相关系数矩阵

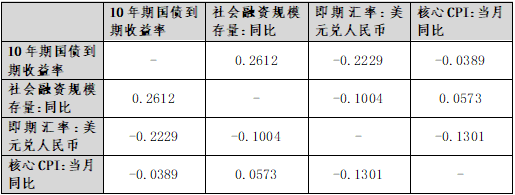
表3：模型残差序列的Durbin-Watson统计量

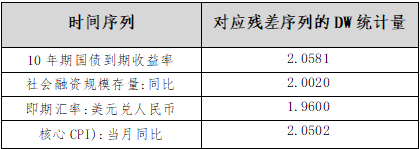
（四）模型预测策略与实施

本研究构建的预测模型，其数据样本覆盖自2016年1月至2021年12月的全面历史数据，旨在为后续时期提供坚实的预测基础。在外推预测阶段，我们选定了2022年1月至2024年5月作为首要考察期，而核心目标则聚焦于对2024年6月至2024年8月这一未来时段的预测。

为实现这一目标，我们采取了双轨制的预测策略：首先，针对2022年1月至2024年5月这一时段，鉴于其已具备完整的真实数据支持，我们采用了滚动外推预测法，即每月根据最新数据更新模型，并仅针对下一月进行预测，以此确保预测结果的时效性与准确性。其次，对于2024年6月至2024年8月的未来三个月，我们则依赖于模型的内生逻辑与前期验证的可靠性，进行了为期三个月的外推预测。

图2清晰呈现了10年期国债收益率在滚动预测期（2022-01至2024-05）内的动态变化，并前瞻性地描绘了未来三个月（2024-06至2024-08）的走势趋势。根据模型的分析与预测，当前10年期国债收益率似乎正处于一个潜在的波谷区域。为量化这一预测的不确定性，我们采用了滚动外推预测期内的平均误差（8个基点）作为预测精度的衡量标准，从而估算出波谷的大致范围可能位于2.32%±8bp之间。

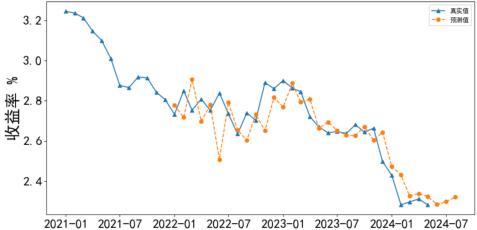
进一步地，模型预测指出，在未来三个月内，国债收益率有望呈现持续回升的态势，这一预测结果与后续章节中的宏观经济分析判断不谋而合，进一步增强了预测结果的可信度与说服力。然而，值得注意的是，由于外推预测在涉及较长时间跨度时误差会自然增大，因此本文在利率反弹高点的具体数值上保持了谨慎态度，未做明确预判。

（五）脉冲响应和方差分解分析

在解析VAR模型中变量间复杂关系时，脉冲响应分析和方差分解是两大关键工具。脉冲响应分析展示了当一个变量受到冲击时，它如何引起其他变量的一系列连锁反应，清晰描绘出动态影响的路径。另一方面，方差分解通过精确量化，计算了每个冲击对变量波动所产生的具体贡献比例，为深入理解系统内部的动态机制提供了可靠的数据基础。

1.脉冲响应分析：量化动态影响

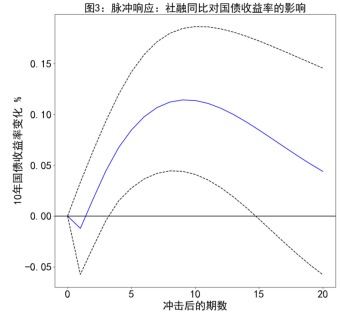
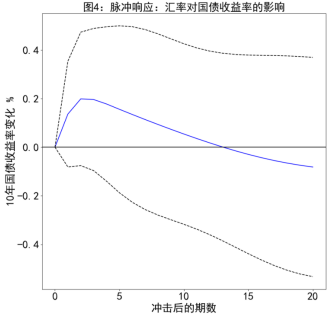
针对构建的VAR模型，我们执行了细致的脉冲响应分析，具体结果见图3至图5。分析过程在95%置信区间内进行，确保了响应结果的可信度。分析显示，10年期国债收益率对汇率和核心CPI的变动有显著响应。在短期内，汇率变动是主要影响因素，尽管其长期影响逐渐减弱并可能转变为负向。相比之下，核心CPI的初期影响较为平缓，但随时间逐渐增强并趋于稳定，展现了其稳定且持久的影响特性。另外，社融同比增速对10年期国债收益率的影响表现为温和且逐步增强，在第8期达到最大影响后逐渐减弱，这表明市场融资情况对长期利率的调节存在时间延迟。

2.方差分解分析：波动成因与贡献度量化

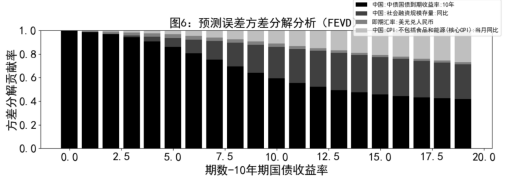
方差分解分析进一步揭示了10年期国债收益率波动的具体成因及各变量的贡献程度。如图6显示，国债收益率的波动主要源自其自身惯性，但随时间推移，惯性因素的影响逐渐减弱，最终稳定在约38%的水平，这反映了市场利率的自我调节与稳定机制。同时，社融同比增速作为重要的外部冲击源，对国债收益率波动的贡献度稳定在28%左右，凸显了金融市场融资活动对长期利率的显著影响。此外，美元兑人民币即期汇率的初期影响显著，但随后迅速减弱至可忽略不计，表明汇率变动对利率的影响具有短期性和非持续性特征。最后，核心CPI则展现出持续增长的影响力，最终稳定在约30%的贡献度，强调了通货膨胀预期在推动长期利率变动中的重要作用。

三、策略展望及模型总结

鉴于当前经济基本面呈现疲弱态势，金融数据与通胀指标的低迷共同指向了市场需求的不足。为维持经济活力，货币政策预计将持续保持宽松。然而，汇率承压及债券市场长端品种投机交易的活跃，反映出市场存在的不稳定性。从央行预告国债借入操作来看，相较于经济增长，防风险和保汇率似成央行当前工作重心。10年期国债收益率在2.25%左右受到政策面的强力支撑。

基于以上宏观经济分析与VAR模型的外推预测，本研究预期下半年10年期国债收益率或面临回升趋势，但其上升空间或受到多方因素制约而显有限。在固定收益资产配置的视角下，建议投资者采取适度控制久期的策略，耐心等待10年期国债收益率上行10-20个基点时的配置机会。

此外，VAR模型分析进一步强调了社融同比增速与核心CPI对10年期国债收益率的深远影响，同时短期内汇率波动的敏感性亦不容忽视。鉴于金融市场极端事件可能引发的尾部风险，需保持高度警惕，因为在此类情境下，VAR模型的预测能力可能受到一定限制，需结合其他风险管理与决策工具进行综合考量。

参考文献

[1]谢添、阮珂、赫然.10年期国债收益率趋势的研判——基于宏观经济分析与时间序列模型预测.货币市场: 2023(08):56-59.

[2]叶青青.基于VAR模型的中国国债收益率宏观经济因素影响研究[D].华东交通大学,2021.

[3]郭济敏,张嘉为.基于Nelson-Siegel模型预测中债国债收益率曲线形态[J].债券,2016(07):66-72.